Lernauftrag 14: KV-Diagramme
Hier findest du die Lösungen.
Die disjunktive und konjunktive Normalform können zuweilen sehr lang werden und stellen nicht die optimale Funktionsgleichung einer Wertetabelle dar. Um kürzere Funktionsgleichungen zu finden nutzt man sogenannte Karnaugh-Veitch-Diagramme (KV-Diagramme).
Bisher haben wir in den Wertetabellen immer eine feste Anordnung der Eingangsvariablen verwendet, zum Beispiel
| \(x_1\) | \(x_0\) | \(y\) |
|---|---|---|
| 0 | 0 | |
| 0 | 1 | |
| 1 | 0 | |
| 1 | 1 |
Bilden wir die zweistellige Dualzahl \((x_1x_0)_2\) und ermitteln ihren Dezimalwert, so sehen wir, das jede Zeile eine eineindeutige Nummer hat und diese aufsteigend ist:
| Nr | \(x_1\) | \(x_0\) | \(y\) |
|---|---|---|---|
| 0 | 0 | 0 | |
| 1 | 0 | 1 | |
| 2 | 1 | 0 | |
| 3 | 1 | 1 |
Dasselbe Prinzip funktioniert auch mit mehr Eingangsvariablen.
Die Werte der Spalte \(y\) lassen sich nun in einem KV-Diagramm für 2 Eingangsvariablen anordnen, in der Form
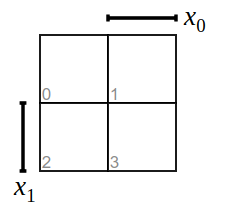
Die schwarze Striche an \(x_0\) und \(x_1\) zeigen an, wo die jeweilge Eingangsvariable in der Wertetabelle 1 ist.
Beispiel
| Nr | b | a | x |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 2 | 1 | 0 | 1 |
| 3 | 1 | 1 | 0 |
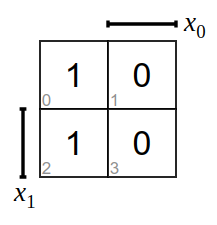
Blockbildung
Nachdem die Ausgangswerte in das Diagramme übertragen wurden, werden benachbarte Felder mit 1 zu Blöcken zusammengefasst. Blöcke dürfen dabei immer nur 2, 4, 8 (Potenzen der 2) Kästchen umfassen. Felder mit Einsen dürfen zu mehreren Blöcken gehören. Ziel ist es möglichst große Blöcke zu bilden und damit alle vorhandenen Einsen zu überdecken.
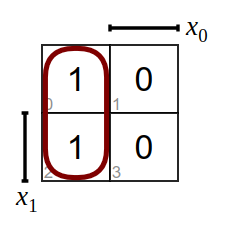
Nachdem alle Einsen überdeckt sind, werden die Eingangsvariablen abgelesen, welche den Block definieren. Hier im Beispiel \(\overline{x_0}\), \(x_1\) und \(\overline{x_1}\).
Wenn eine Eingangsvariable und ihre Negation in der Auflistung auftaucht, so wird diese weggelassen. In diesem Beispiel fallen \(x_1\) und \(\overline {x_1}\) raus und somit das Ergebnis \(y=\overline{x_0}\)
Algorithmus
- alle Ausgangswerte der Wertetabelle ins entsprechende KV-Diagramm übertragen
- möglichst große Blöcke von Einträgen mit 1 bilden (Blöcke können immer nur 2, 4, 8 usw. Kästchen umfassen)
- Funktionsgleichung der Blöcke ablesen (Eingangsvariablen mit \(\land\) verknüpfen, Eingangsvariablen die ihre Negation mit enthalten werden weggelassen)
- Die entstandenen Terme mit \(\lor\) verknüpfen
1. Beispiel für 3 Eingangsvariablen
| Nr | \(x_2\) | \(x_1\) | \(x_0\) | \(y\) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 2 | 0 | 1 | 0 | 0 |
| 3 | 0 | 1 | 1 | 0 |
| 4 | 1 | 0 | 0 | 1 |
| 5 | 1 | 0 | 1 | 0 |
| 6 | 1 | 1 | 0 | 1 |
| 7 | 1 | 1 | 1 | 0 |
In ein KV-Diagramm übertragen
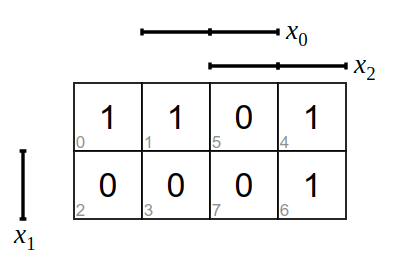
und zu Blöcken zusammengefasst
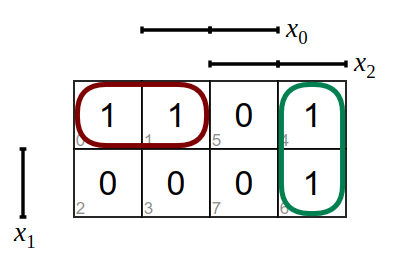
und erhält als Funktionsgleichung
\(y=(\overline {x_1}\land\overline{x_2})\lor(\overline{x_0}\land x_2)\)
2. Beispiel für 3 Eingangsvariablen
| Nr | \(x_2\) | \(x_1\) | \(x_0\) | \(y\) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 1 |
| 3 | 0 | 1 | 1 | 0 |
| 4 | 1 | 0 | 0 | 1 |
| 5 | 1 | 0 | 1 | 0 |
| 6 | 1 | 1 | 0 | 1 |
| 7 | 1 | 1 | 1 | 0 |
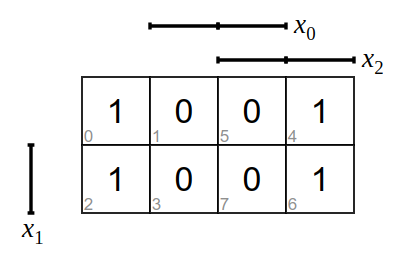
Blöcke können auch über die Grenzen des Diagramms hinaus gebildet werden.
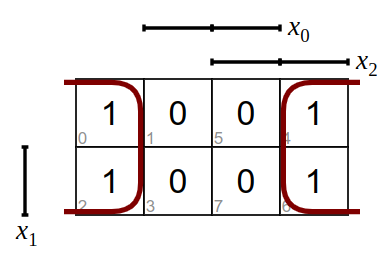
und erhält als Funktionsgleichung:
\(y=\overline{x_0}\)
1. Beispiel für 4 Eingangsvariablen
| Nr | \(x_3\) | \(x_2\) | \(x_1\) | \(x_0\) | \(y\) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 2 | 0 | 0 | 1 | 0 | 1 |
| 3 | 0 | 0 | 1 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 | 0 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 7 | 0 | 1 | 1 | 1 | 0 |
| 8 | 1 | 0 | 0 | 0 | 1 |
| 9 | 1 | 0 | 0 | 1 | 1 |
| 10 | 1 | 0 | 1 | 0 | 1 |
| 11 | 1 | 0 | 1 | 1 | 1 |
| 12 | 1 | 1 | 0 | 0 | 0 |
| 13 | 1 | 1 | 0 | 1 | 1 |
| 14 | 1 | 1 | 1 | 0 | 0 |
| 15 | 1 | 1 | 1 | 1 | 0 |
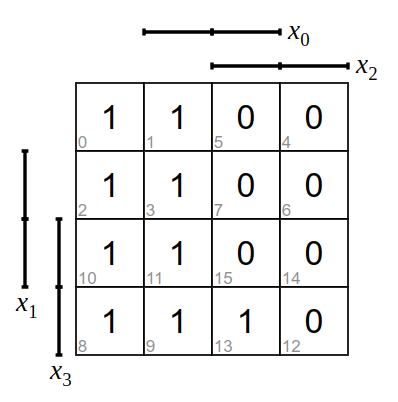
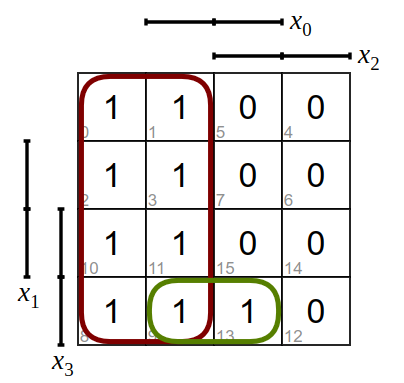
und ergibt als Funktionsgleichung
\(y=(\overline{x_2})\lor(x_0\land\overline{x_1}\land x_3)\)
Aufgabe 1
Bilde zu den folgenden KV-Diagramme die Funktionsgleichung und zeichne die logische Schaltung.
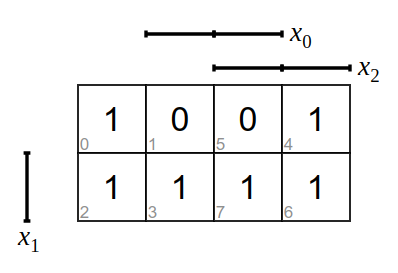
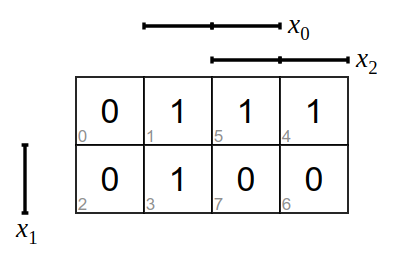
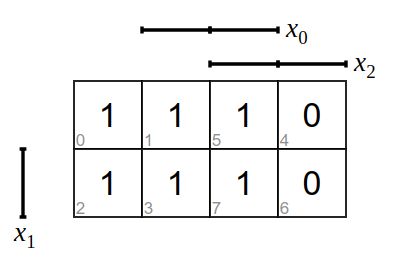
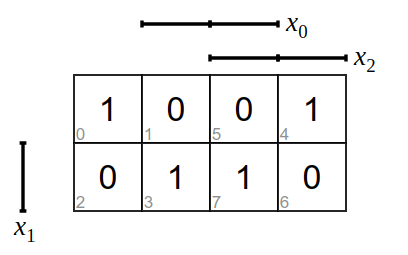
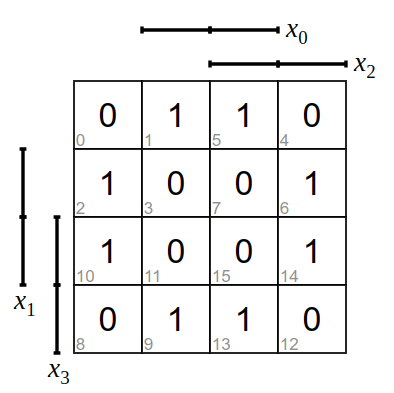
Aufgabe 2
Bilde zu den folgenden KV-Diagramme die Funktionsgleichung und zeichne die logische Schaltung.
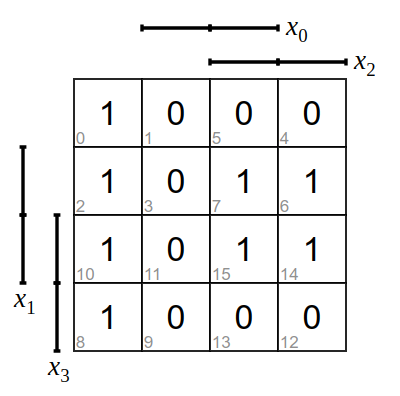
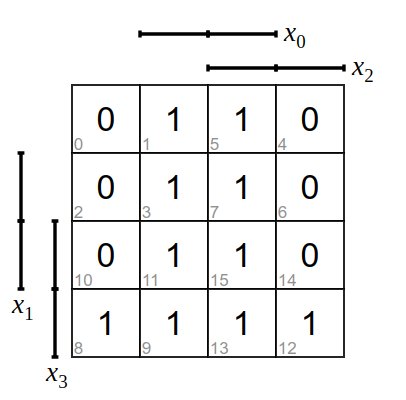
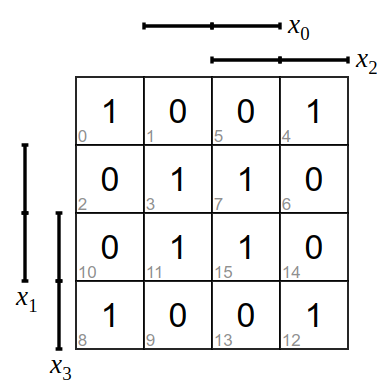
Weiter zur nächsten Lernaufgabe